
루트(Root)라는 하나의 꼭짓점 데이터를 시작으로, 여러 개의 데이터를 간선으로 연결.
각 데이터를 노드(Node)라고 하며, 두 개의 노드가 상하 계층으로 연결되면 부모/자식 관계를 가진다.

[Tree의 노드 관계도]
노드(Node) : 트리 구조를 이루는 모든 개별 데이터
루트(Root) : 트리 구조의 시작점
형제 노드 : 부모가 같은 노드
부모 노드 : 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에 가까운 노드.
자식 노드 : 두 노드가 상하관계로 연결되어 있을 때, 상대적으로 루트에서 먼 노드.
리프 노드 : 트리 구조의 가장 끝 지점이며 자식 노드가 없는 노드.
차수 : 특정 노드가 가지는 자식 노드의 개수.

[Tree 용어]
1. 레벨(Level) : 같은 깊이를 가지고 있는 노드들의 묶음. 같은 레벨의 노드들은 형제 노드라고 부른다.
2. 깊이 (depth) : 루트로부터 하위 계층의 특정 노드까지의 간선의 개수.
A의 깊이 : 0, B,C의 깊이 : 1, D,E,F,G의 깊이 : 2
3. 높이 (height) : 리프 노드(자식 노드가 없는 노드)를 기준으로 루프까지의 높이.
부모 노드는 자식 노드의 가장 높은 height값에 +1값을 높이로 갖는다.
H, I, E ,F J의 높이 : 0, D,G의 높이 : 1 B,C의 높이 : 2 A의 높이 3
4. 서브 트리 (Sub Tree) : 트리구조의 root에서 뻗어 나오는 큰 트리의 내부에, 트리 구조를 갖춘 작은 트리
[Binary Search Tree] 이진 탐색 트리

자식 노드가 최대 2개인 노드로 구성된 트리. 부모 노드를 기준으로 작다면 좌측, 크다면 우측에 위치.
[Tree traversal] : 트리 순회
특정 목적을 위해 트리의 모든 노드를 방문하는 것. 방문은 무조건 왼쪽부터 오른쪽 순으로 진행한다.
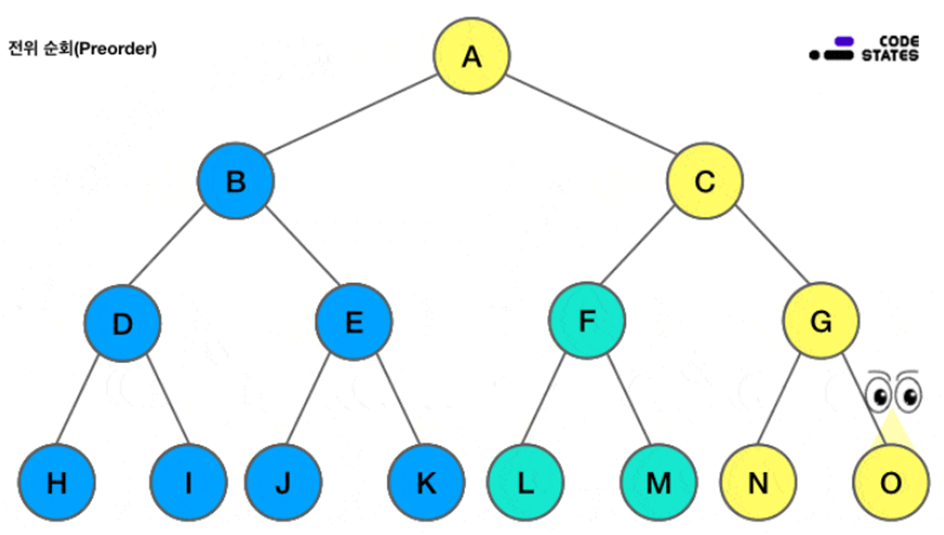
[1] 전위 순회 (preorder traverse)
(좌측의 기준) 자기 자신 -> (좌측의) 자식 > (우측의) 자식 순으로 순회
A -> B -> D -> H -> I -> E -> J -> K -> C -> F -> L -> M -> G -> N -> O
[2] 중위 순회 (inorder traverse)
루트 기준 좌측의 자식 끝부터 순회 > 자신 > 우측자식 > 다음 자신 >좌측자식 > 우측 순으로 순회
H -> D -> I -> B -> J -> E -> K -> A -> L -> F -> M -> C -> N -> G -> O
[3] 후위 순회 (postorder traverse)
루트 -> 좌측 자식 > 우측자식 > 자신 순서로 순회
H -> I -> D -> J -> K -> E -> B -> L -> M -> F -> N -> O -> G -> C -> A
[실제 트리 순회 코드 작성 예시]
(1)
(2) (3)
(4) (5)
[1] Node 클래스를 선언하고 이진탐색트리의 노드인 : left, right, data 를 필드 변수로 선언.
class Node {
int data; 자기자신.
Node left; 좌측_자식_노드
Node right; 우측_자식_노드
}
[2] Tree 클래스를 선언하고 필드 변수로 root 선언하고
메인 클래스에서 불러올 수 있도록 생성자 Node를 통해 get/set 설정.
class Tree {
public Node root;
public Node getRoot() {
return root;
}
public void setRoot (Node root) { // setRoot를 입력하면 변수명을 root로 지정한다.
this.root = root;
}
}
[3] 노드 클래스에 선언했던 Tree의 주요 요소인 left, right, data 노드를
Node 생성자로 선언하고 메소드의 매개 변수로써 할당하도록 하여 메소드를 생성.
public Node(생성자) makeNode (Node left, int data, Node right) {
Node클래스에 선언한 필드들을 매개변수로 사용해서 만들어야 하므로, Node클래스(생성자)로 메소드 생성.
Node node = new Node(); // 노드 클래스를 기반으로한 node 객체 선언,
node.data = data;
node.left = left;
node.right = right;
Node 클래스의 객체인 node를 통해 Node클래스의 변수명과 해당 메소드의 매개변수가 같음을 this. 키워드로 선언.
return node;
}
[4] 3가지 순회 방법에 따라 메소드 생성. // 재귀호출을 활용.
public void inorder (Node node) { (중위 순회로써, 좌측 자식 ->자기 자신 -> 우측 순으로 순회)
if ( node != null ) { // node가 빈 상태가 아닐때 까지 반복,
inorder(node.left); // 좌측 노드 생성의 재귀호출
System.out.println (node.data); // 나 자신을 호출
inorder (node.right); // 우측 노드 생성 재귀호출
}
}
public void preorder (Node node) { (전위 순회로써, 자기 자신 -> 좌측 -> 우측 순으로 순회)
if ( node != null ) { // node가 빈 상태가 아닐때 까지 반복,
System.out.println (node.data); // 나 자신을 호출
preorder(node.left); // 좌측 노드 생성의 재귀호출
preorder (node.right); // 우측 노드 생성 재귀호출
}
}
public void postorder (Node node) { (후위 순회로써, 좌측 -> 우측 -> 자기자신 순으로 순회)
if ( node != null ) { // node가 빈 상태가 아닐때 까지 반복,
preorder(node.left); // 좌측 노드 생성의 재귀호출
preorder (node.right); // 우측 노드 생성 재귀호출
System.out.println (node.data); // 나 자신을 호출
}
}
[5] main 클래스에서 트리의 시작점인 root가 있는 Tree클래스의 객체 선언.
public static void main (String[] args) {
Tree t = new Tree(); // Tree 클래스 객체 t 선언.
** (트리의 시작점 root와 노드를 만드는 makeNode 메소드, get/set root가 포함된 클래스 Tree를 객체 선언)
Node n4 = t.makeNode(null (좌측노드), 4(data 자기자신), null(우측노드));
Node n5 = t.makeNode(null (좌측노드), 5(data 자기자신), null(우측노드));
Node n2 = t.makeNode(n4 (좌측노드), 2(data 자기자신), n5(우측노드));
Node n3 = t.makeNode(null (좌측노드), 3(data 자기자신), null(우측노드));
Node n1 = t.makeNode(n2 (좌측노드), 1(data 자기자신), n3(우측노드));
t.setRoot(n1); // ** n1 노드를 root로 선언.
t.inorder(t.getRoot()); // ** inorder 메소드 실행.
** inorder 메소드는 node를 매개변수로 필요하니 root가 있는 클래스의 객체인 t를 활용하여
트리의 시작점인 root를 호출하는 get 메소드로 실행
}
'백엔드 학습 과정 > Section 2 [재귀함수, 자료구조, 네트워크]' 카테고리의 다른 글
| #4. 웹 ( WEB ) - 웹아키, 웹앱-아키, 웹앱-요청흐름, 웹앱요소,HTTP, SSR&CSR, Message(+패킷), 쿠키,세션,캐시,프록시 (0) | 2022.12.03 |
|---|---|
| #3. 네트워크 [프로토콜, TCP/UDP, IP&MAC, PORT, URL,URI, DNS] (0) | 2022.11.30 |
| #2-2 자료구조 - Graph (0) | 2022.11.23 |
| #2-1 자료구조 - Stack, Queue (0) | 2022.11.23 |
| #1. 재귀함수 (0) | 2022.11.22 |



